ブログ

皆さん、こんにちは！

塾講師を経験しておりました登録講師です。今日は子育てについて書いていきたいと思います。

数学が苦手！という方や子供が数学嫌いという方は多いのではないのでしょうか。

「思うように問題が解けない」とか「たくさん勉強したのにテストの点数が伸びなかった」など様々な経験があると思います。そんな方のために、本日お話したいことはまさに算数・数学の勉強法です。 どんなスポーツだってコツがあるように、どんなゲームだって攻略方があるように、数学にも得意になるための取り組み方があります。

確かに学校では成績を計るものはテストの点数で、テストにおいて求められるのは基本的に解答です。しかし、数学に取り組むときに大切なのは解がどうかではありません。 社会などの暗記型の科目では、キーワードを知っていれば点数を取ることが出来ます。しかし、数学では、「数学の問題が解ける≠答えを知っている」と言えます。数学が得意な人はこれから話す、数学に取り組む姿勢がしっかりとできているからなのです。

 

取り組む意識を変えれば数学に対する意識が変わってくるかもしれません。 どんなことでもそうですが、出来ると楽しいですからね。

子どもになってみよう。

突然ですが、子供の頃に車で出かけた時のことを思い出してみてください…

目的地に向かっている途中、皆さんは車の中で何をしていましたか？誰かとお話したり、お菓子を食べたり、ゲームをしたり、ひたすら寝たり…色々ありますよね。
目的地について、お買い物をして、遊んで思いっきり楽しむ！目的地が目的。その道中は気にならないことがほとんどだと思います。

ただ、少し大きくなって、恋人ができて、カワイイ彼女（カッコイイ彼氏）をその場所に連れていきたい！となったときに、「行ったことある」から迷うことなく行けるでしょうか？

調べることなく迷わず目的の場所へ行けるかどうかは道（行き方）を知っているかどうかです。つまり、一度行ったときにその道中で

「どの道を通ったのか」
「目印となる建物などは何だったのか」
「どのくらいかかったのか」

などを気にしていたならば、一人でもたどり着ける可能性は高くなります。実は算数・数学を勉強するうえではこの考え方がとても大切なのです！！

道のりが大切。

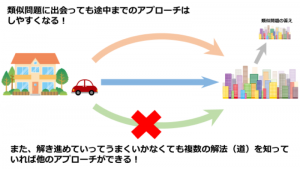
目的地（解答）がわかっていてもそこまでの道（解き方）がわかっていないと結局一人では問題は解けるようにならないのです。
様々な生徒に教えてきた中で、「とりあえず答えを知りたい！」という子はたくさんいました。 考えてもわからないから答えをすぐに見てしまう、ノート提出があるからとりあえず答えを写しておく…。ちなみに、私はいけないことだとは思いません。ただ、それで終わってしまうから中々解けるようにならないのではないでしょうか。

数学好きな私の知人も学生時代の勉強では、わからない問題があったらまず答えを見ていたと言っていました。得意だからといって、なんでもかんでも答えが出せるわけではないのです。
これはつまり目的地（解答）の確認ですね。そこから逆算して、どの道順で向かうのがわかりやすいのか（どうやって答えを導いたのか）、他に良い道はなさそうか（ほかの解法はないか）などを考えるのです。

そうやって道のりについて考える癖をつけておくと、類似問題と出会っても一人で解けるような力がついていくのです。

 

 

とある生徒が言った一言…

塾で教えていたころ中学生の女の子に言われたことがあります。

「先生は1から１０のうちの3から6を教えてくれるから、数学を勉強していて楽しく感じる！」

それは教える時に強烈に意識していたことで、その子の発言があまりに的確すぎて、末恐ろしい子だとおもいました。でもこれはまさに今回の話の内容において重要なポイントになることでもあります。教えるのに1から10まで段階があったとして、1や2は解くうえで基本となるようなこと。ここを丁寧に説明されても飽きてしまう子が多いのです。近所だったら教えてもらわなくても道はある程度知っていますよね。案内されても「知っているし…」となってしまうわけです。逆に、7から10は解く方針が立って答えに向かっていく段階。つまり、目的地が見えるくらい近くまで来ればそこからは自分の力で近づいていくことが出来るということです。ここは時間がかかっても本人にやらせるべきです。快適なまま目的地に導いてはいけないと思います。
結局、教育が担っているのは３から６の「道」を教えてあげることなのです。一旦3から6は導いてあげて、次に1から10までやらせてみる。こうやって出来るようにさせてあげるときっとテンポ良く、楽しく勉強ができるのです。『考える力』を奪ってはいけないんです。

まとめ

この話は、当たり前のことを言っているように聞こえる方もいると思います。しかし、自身の勉強だけでなく、お子さんや生徒さんに勉強を教える時に意識してみるときっと数学が好きになっていってくれるはずです！
自身の勉強はもちろん、学校の授業もそういった視点で聞いてみると違った受け方ができるかもしれません。

数学が解けるのってすごく楽しいですよ！

ではまた次の記事でお会いしましょう。

皆さんこんにちは！本日は「生態学と数学のかかわり」についてお話したいと思います。

生態学とはどんな学問かというと、「生物と環境の間の相互作用を扱う学問分野」です。つまり、生物の体内で起こっていることではなく、その生物自体が、生息している環境や集団に、どのような影響を及ぼし、どのような戦略を持って生きているのかを突きつめていく学問です。さらに、生態学の中に「行動生態学」という分野があります。動物の行動について実験・観察をしていき、行動の原因を探っていく学問です。野生の生き物を調査しに山や島に籠ったり、特別な環境下での生き物の行動を記録し続けたりと、根気と体力が必要な分野といえます。実験手法の関係上、24時間寝ずに1匹の昆虫を観察し続けたりすることもあります！

 

行動生態学の分野には現象の原因として4つの理由（要因）を考えます。 今回はそのうちの2つの要因についてお話しようと思います。

 

鳥はどうして渡りをするの？？

「鳥はどうして海を越えるような長い距離を飛んで渡りをするのか？」

 

皆さんはこの疑問に対してどのような答えを考えますか？

「冬の間は子育てのために暖かい場所へ移動するんだ」
「海の向こうにまだ見ぬ何かがあるから…」

もしくは

「季節変動によって変化する日長時間を体内のセンサーが感じ取り、特定のホルモンが分泌されて生理状態が変化することにより、渡りが行われる」

どれも正しそうです。 一つの疑問に対して様々な角度から答えを考えることができますね。

「そんなもの鳥に聞いてみないとわからない！」

と思った方もいるかもしれません。
今回お話したいのは今挙げた回答例のように、行動生態学には一つの現象に対して色々な要因(factor)が考えられ、それぞれが影響していると説明することができるということです。
先に４つある要因中から代表的な２つの要因をあげると言いましたが一つ目がこれです。

至近要因(proximate factor)

これは現象がどのような仕組みで起こっているかという観点から考えたものです。
鳥の渡りの例でいうならば、「季節変動によって変化する日長時間を体内のセンサーが感じ取り、特定のホルモンが分泌されて生理状態が変化することにより、渡りが行われる」という答えです。

例えば「あいちゃんはなぜ恋に落ちるの？」という現象の至近要因は、辰人君から得られる感覚的な情報に対して、脳内で特定のホルモンが分泌され、拍動が早くなったり、性ホルモンが分泌されることにより、恋に落ちたと感じるからとなります。なんかロマンティックじゃ無いですね(笑)

 

それに対して、現象が生存・繁栄のためにどのような機能を持っているかという観点から考えたものが２つ目の要因で

究極要因(ultimate factor)

鳥の渡りに関しては、まだわかっていないことが多いですが、「餌の確保」や「繁殖行動と子育て」が目的だと思われます。生物（各個体）の究極の目的は種の保存です。つまり、子孫が何世代にもわたり継続し、遺伝子が引き継がれていくことが重要なのです。よって究極要因を考えることは生物を理解する上でとても重要なのです。

究極要因と統計学

至近要因については、物理学や生化学といった学問から、特定の物質や反応の過程を調べることによってある程度の答えを導くことが出来ます。

では、究極要因についてはどうでしょうか？もし、対象がヒトであれば「なぜ？」と聞くことが出来ます。しかし、ヒト以外の生物となると「なぜ？」と聞いても答えは分かりません。だからといって、犬語や猫語、鳥語…と勉強するわけにもいきませんよね。

究極要因を考えるためには、2つの視点があります。

① 「生存」に有利かどうか

② 「繁殖」に有利かどうか

まず、前提として生物には個体差が存在します。

”ある行動”について、その有無、強弱、タイミングなどは個体によって異なってくるのです。つまり、この行動の個体差が生存率や繁殖成功率にどう影響しているのかを調べるのです。「生存」に直結する行動であれば、生き残るのは”ある行動”を選択した個体が大部分になるため、観察と追跡によって考察をしていくことが多いのです。

基本的に生物の行動は自然淘汰的に有利な行動が選択されていきます。また、個体は「種のため」に行動せず、それぞれが「自分自身にとって」有利な行動をとっていくことで淘汰が起こります。鳥の渡りについても、渡りをしない個体があればエサがなくなったりして死んでしまうでしょう。渡るということが自分自身にとって有利に働くため、全体が渡りという行動をとるようになっていったのです。

仮に渡りをしない個体が種内にいたとして、その後を観察した結果、大部分が死んでしまうのであれば、その行動は「生存」に関して必要な行動だということです。死んでしまった原因を調べれば、その行動の究極要因が考察できます。
「繁殖」に関わる行動については、その行動が生殖行動とどう連動しているかを観察します。しかし、それだけでは憶測の域を出ませんので、繁殖成功率についてデータをとって検証していくことが重要になります。

ここで活躍するのが統計学です。

“ある行動”によって、「繁殖成功率に変化はない」と仮説を立て、その生物の観察からデータを収集します。そして得られたデータに対して統計的な手法を用いて、行動が「個体が存続していくために有利であろう」ことを導くのです。ここでは例えば母比率の差の検定を行います。

母比率の差の検定では、2つのグループの「繁殖行動が成功したか否かの比率」が等しいかどうかを調べるときに使います。2つのグループの標本数をそれぞれm、nとし、

その成功比率を，とします。 このとき、

帰無仮説：行動による繁殖成功率に差はない（=）

対立仮説：行動によって繁殖成功率に差がある

となり、以下の式で求められる検定統計量Zが標準正規分布に従うことを利用して検定を行います。

ここで、は2つのグループの比率の加重平均で、以下の式で求めます。

求められた検定統計量Zについて、標準正規分布表を使って設定した有意水準の有意点の値と比べて判定をします。
このようにして偶然ではなく統計的有意に繁殖成功率が高くなることを示すのです。

例えば、ホタルが光る理由。

至近要因は「ルシフェリンが…」となりますが、究極要因としては「メスをおびき寄せて交尾をするため」です。（危険を察知した時にも光を発しますが、光り方が違います）
ここで、「光ることで繁殖成功率に差は出ない」という仮説のもと、光を発する頻度、間隔、時間帯、強さなどのデータを取り、それぞれについて生殖行動に繋がったかを複数個体で記録します。
その上で、例えばそれぞれの行動について、頻度の高い・少ない、間隔の長い・短いなどのグループに分けて繁殖成功率の差を検定します。
その結果から、有意差が出れば、光ることが繁殖成功率に影響することが分かります。また、繁殖成功率と各行動頻度の散布図を作成して相関関係があるかを調べてみるとさらに関連性も見えてきます。

このように、様々な生物には直接聞けないからこそ、統計という学問の力を借りて原因を突きつめていくのですね。
皆さんが普段テレビなどで見る動物番組の情報は、こういった「地道な観察」と「統計学の活躍」があるからこそ伝えることができているのです！

まとめ

仮説を検証するためには、相当綿密な計画を立てなくてはいけません。 生物が生息している環境内では、影響を及ぼす因子が無数に存在します。それらを一つずつ取り除いていき、特定の因子が現象とどう関わっているかを確かめられていなくては実験が破綻してしまいます。ホタルの例だって雌の密度によって雄の光り方が変わるかもしれません。 しかし、生態学では、1年を通していつでも実験・観察が出来るわけではありません。その生物の発情時期が決まっていたり、出現する時期が決まっていたりするためです。一所懸命考えて立てた計画にもとづいて研究を進めても、ある一点で破綻があると、次のチャンスは1年後となってしまうことも起こりえます。結果まである程度シミュレーションをしたうえで、万全の準備が必要なのです!!

本日のお話では生物に見られる行動、現象の４つの要因の２つのみを紹介しました。その２つについて詳しく、また今日紹介できなかった残りの要因について書いてある本を紹介しておきます。

生き物をめぐる４つの「なぜ」/長谷川眞理子

では、また次の記事でお会いしましょう。

大人なら昔、誰でもやったことがあるであろう、スーパーやゲーセンなどにあるじゃんけんゲーム。勝てばコインをもらえるというルールでとても単純ですがはまってしまうゲーム機で子供に大人気でした。
じゃんけんゲームはあいこの場合はゲームが続くため「勝ち」か「負け」しか存在しません。勝てばルーレットが周り出た数字の枚数だけコインがもらえます。一方負けたら入れたコインが没収されます。マシンによりますが、勝てば最大50枚のコインがもらえるなんて言うものもあります。しかしなぜかみんな最終的にコインは0になってしまいます。

色々なマシンがありますが、よく街で見るマシンについて解説します。勝ちの場合の配当ですが、

1枚が2つ
2枚が4つ
4枚が2つ
7枚が2つ
16枚が1つ
50枚が1つ

の計6種類（12ゾーン）。上記でも示したようにあいこだとゲームが続くので結果は「勝ち」か「負け」しかありません。ルーレットの止まる確率が均等だとしたら勝った時にコインがもらえる期待値は

より、8.17枚が期待収益として得られます。普通のギャンブルだと胴元が必ず儲かるように調整しているので、勝率がもし50%だとすると配当は2倍より小さくなるように調整しています。
配当を2倍より小さくしておけば、胴元の期待収益がプラスになるからです。

しかし、じゃんけんゲームの場合だと8.17倍という常識では考えられないくらい大きな数値が出ます。
これが現金での配当ならみんな億万長者になってしまうことでしょう。しかし、じゃんけんゲームの場合最終的にみんなコインが0になります。なぜでしょうか。
それは下記の4つのことが考えられます。

• ルーレットの出る目が均等ではない
• 勝率が1/2ではない
• 確率階層を含むゲーム
• 0枚になるまでやめない

ルーレットの出る目が均等ではない

ルーレットはダーツの的のように等しい角度で分割されていますが確率は均等かどうかは怪しいのです！
つまり12個の的がありますがそれぞれの確率が1/12ではない可能性があります。
12勝しても50が出ないということがよくあると言えるでしょう。じゃんけんに買っても勝っても配当が1枚や2枚ばっかりだと配当の平均値は減ります。

勝率が1/2ではない

果たしてじゃんけんの勝率は1/2なのでしょうか？こちらがボタンを押さなければ

じゃ～んケーン

じゃ～んケーン

と、こちらが手を出すのを求めてきます。つまり完全なランダムではなくて”ある一定の確率でじゃんけんゲームが負けてくれている”と考えることができそうです。

確率階層を含むゲーム

そして一番大きい理由がこれです。スマートフォンのゲームでもよくあるのが関門がいくつかあって、それらを抜けるためには確率pの勝負に勝たなければいけず、更に次の関門では確率qの確率で勝たなければいけないというような階層構造で、結果的に一つ一つの確率は勝てそうでもすべての関門を抜けるためには、p×qの確率になってしまい非常に小さくなってしまうというミソです。
先程、期待値を8.17と導出しましたが、実はあくまでじゃんけんに勝ったもとでの期待値です。なので厳密には8.17×1/2=4.085（仮に1/2とします!!）となっているのです。
巷を騒がせたレアガチャ問題もその一つということが出来ると思います。

0枚になるまでやめない

投資戦略の話にもなりますが、仮に勝率1/2で確率的試行を行っている場合、いつかは0になってしまいます。
→ファイナンス数学におけるブラウン運動

例えば「100枚たまったらやめる」というルールを作れば達成する人は多いでしょう。しかし、じゃんけんゲームのコインはそこでしか使えないため全部そこにつぎ込むのです。
結果的に0枚になるまでやり続けることになってしまい、最終的に0枚になる仕組みになっているのです！

まとめ

簡単なゲームの中にも確率が潜んでいる…ことはもう知っていたと思いますが。大切なのは、”簡単な確率”の裏に潜む”難解な確率”を意識しておくことですね。

そして、ギャンブルは勝ったらやめましょう!!

みなさんコンニチハ．
最近はずっとTeXで数学の文書を書きまくっています．
TeXをやっているときって，なんだか時間がものすごく早く過ぎます…
そして，美しい数式のフォルムは，いつ見てもうっとりします…
（もはやTeXオタクすぎて病気かもしれません…）

加法定理はすごいって話

前回ぼくが書いた記事では，三角関数の公式なんぞ，加法定理から導いてしまえ!!
というお話をしました．三角関数の加法定理→種々の公式 という流れには，
数学の本質的な「少数の基本原理→様々な結果」という考え方が
かなり色濃くあらわれているんだよ～，と．

だから，三角関数の加法定理っていうのは，
かなり本質的な「基本原理」だから，これは必ず知っておこうぜ！
というお話をしたところだったのですが…

オイラーの公式

オイラーの公式という，超有名な公式があります．

この式は，指数関数と三角関数のマクローリン展開によって証明されますが，
三角関数と指数関数という，”一見”何の関係もなかった関数が
虚数単位を仲立ちにしてここまで分かりやすく繋がるという，
まぁー，なかなかに感慨深い公式なのです．

この公式に θ=π を代入した式

は，あまりにも有名ですね．（博士の愛した数式という小説でも沢山出てきてましたね)

オイラーの公式が加法定理すら集約する

で，このオイラーの公式っつーのは凄いわけです．
というのも，三角関数の加法定理ってのは，オイラーの公式からちょいっと導かれてしまうのです．

てなわけで，ちょいと本格的な話ですが，
せっかくの数学なんでも相談所ということで，やってみましょう．

これは，オイラーの公式からすぐに分かることなので，す，が．

一方で，指数法則より，

 

最初の式と実部と虚部を比較すれば，実は加法定理が出てきていることが分かりますか？
これは何とも，驚くべきお話です．
加法定理ってのは，初等的に証明すると結構大変な式なんですが，
オイラーの公式は，いとも簡単に導き出しちゃうのです．

オイラーの公式はすごい

ちなみにオイラーの公式ってすごくて，
こういう「え！？そんな簡単に導けちゃうの！？」みたいなことがよく起きます．
たとえば，ちょっとマニアックですが，三角関数のラプラス変換の公式

は，ふつーに定義から導こうと思うとけっこう大変なのですが，
指数関数のラプラス変換

とオイラーの公式と，ラプラス変換の線形性を使うと，これまたあっという間にわかります．

いっぽう，オイラーの公式より，

実部と虚部比べると，もう公式出てきてますよね．
なんとも，オイラーの公式の凄さが実感できる結果です．
こんな感じで，「オイラーの公式で劇的に簡単になること」を探してみるのも面白いですよ．

「すべてがひとつに集約される」楽しさ

数学には「すべてがひとつに集約される」面白さというのがあって，
今回紹介したオイラーの公式に限らず，いろんなところにそういったタイミングが現れます．
それに出会えたとき，数学ってやっぱり面白いなぁ，と
僕は毎回毎回，再認識するのです．

喋り始めるとキリがないのですけどね笑
このブログが，せめて僕の語りの発信場所になれば嬉しいなぁ．

ということでまた次号で！あでゅー！！

数学なんでも相談所 YOROZU屋の明松 真司(あけまつ しんじ)と申します．これからどうぞ，よろしくお願いいたします．

簡単に自己紹介をさせてください！
僕は北海道釧路市に生まれ，釧路高専（工業高等専門学校）を卒業した後に
東北大学の理学部数学科に入学，卒業しました．
現在は，数学好きの教育者をやらせていただいてます．
趣味が講じて「線形空間論入門」という本を出版させてもらったりもしました．この「YOROZU屋」に合流させてもらったのは，とっても最近です．
何だか数学好きが，数学を愛する人達に引き寄せられていったかのように，
本当に偶然，このブログを書かせてもらっているような感じです．
今日はちょっとご挨拶がてら，「数学」とどういうふうに付き合っていて，
「数学」に対してどういうふうに思っている人間なのかを書かせてくださいませ．

数学好きになったのは，高専の3年生のとき

高専の3年生のとき，僕は数学オタクの先生と出会ったのがきっかけで
数学のどんどんどんどん，はまって行きました．
最初に読んだのは，線形代数学の本（「線形代数学大全」）でした．
まさか，当時は自分が線形代数の本を書いているなんて想像していなかったなぁ．

しんどい計算をしなきゃいけないときもあるし，
どんなに考えても全く理解ができないときもあるんだけど，
あるとき急に絡んでいた糸が一気に解けたり，
そのくせ，世界を変えるくらいに役に立ったりする．
リアリティとスリルがあるこの「数学」という学問は，
自分の中では，他に代わりが見つからないくらいに大切な趣味です．

世の中には，数学を必要としている人がたくさんいる

僕は数学が「面白い」から，たくさんたくさん数学をやっている人間なのですが，
「面白い」と同時に，数学は途轍もないくらいに役に立ちます．

たとえば，我々はデータというものと対峙することがあります．
アンケートの結果だったり，テストの点数だったり，
顧客からのコンバージョンの数だったり，花弁の長さだったり…

そして，データって「整理」をして，「傾向」を見たくなるんです．
でも，そこが「なんとなく」だと，我々は「見かけ」に騙されてしまうかもしれない．
「直感」と「真実」がズレることは，この世界では日常茶飯事です．

では我々は，そこからどうやって「真実」を取り出せば良いのか？
統計学(statistics) を使うんです．
この数学が，我々に「本当と嘘」を数字で教えてくれます．

(正規分布による確率の計算)

よく経済ニュースを見ることがあると思います．
経済学ですら，そのベースは数学です．

(経済学での「弾力性」の数学的定義)

CDは，ちょっとくらい傷がついても聴けるし，
電話も，ちょっとくらいノイズは入るけど問題なく通話ができますし，
QRコードも，てきとーに読み取ればきちっとURLが表示されます．
そのバックグラウンドには，誤り訂正符号(error correcting code)という理論があって，
それは驚くほど純粋な数学（純粋数学）によって支えられています．

(Hamming符号の検査行列)

世の中には，数学を必要としている人がたぶんたくさんいる

数学って，こんな感じで面白いし役に立つんですが，
なんせちょっと敷居が高いんです．
面食らってしまう人も多いと思いますし，
よく分からずにあきらめてしまう人も多いと思います．

学生時代，何がしたいのか全く分からずに「数学」が
目の前を通りすぎてしまった人って多いと思うんですよ．
でも，そのくせ何かと必要に迫られる厄介な奴だなぁ…
って思われている方も，きっと多いと思います．

だから，僕達「YOROZU屋」が，そのときに「助け」になれたら
この上ない幸せだなぁと思っています．
困ったときは，いつでもお声がけくださいませ m(_ _)m

そんなわけで

このブログではこれから，数学の話や，教育の話などなど，
わりとフリーダムに，好きなこと書かせていただこうと思っております．

しっかり役に立つ，しっかり使える数学も，
なんだか面白い，美しい数学も，
YOROZU屋は，皆さんにお伝えして行くことができると思っています．
それはこのブログを通じてかもしれませんし，
直接皆さんに，かもしれません．どちらにせよ，我々は全力ですm(_ _)m

これから「数学なんでも相談所 YOROZU屋」を，よろしくお願いしますねー！

ではでは．明松真司でした．